Federated learning (FL) trains a model across clients without sharing raw data. FLICKER uses CKKS homomorphic encryption to privately address class imbalance. However, the cosine values shared during resampling can leak enough geometric information to reconstruct data points—especially in low dimensions.
TL;DR: If you know the cosines between an unknown point and enough known directions, the unknown is confined to the intersection of cones. In low dimensions this identifies the direction; simple metadata then fixes scale/sign to yield the original point.
Geometric idea
For unit vectors \(u_i\) and a unit direction \(y\), each cosine \(c_i = u_i^\top y\) defines a cone with axis \(u_i\) and opening angle \(\theta_i=\arccos(c_i)\). The feasible set is \[ \mathcal{F} = \Bigl\{\, y \in \mathbb{R}^d \;:\; u_i^\top y = c_i \ \forall i \Bigr\}. \] With \(k\) independent constraints, \(\dim(\mathcal{F})=d-k\). When \(k=d\) and the rows are independent, \(\mathcal{F}\) collapses to a line through the origin.
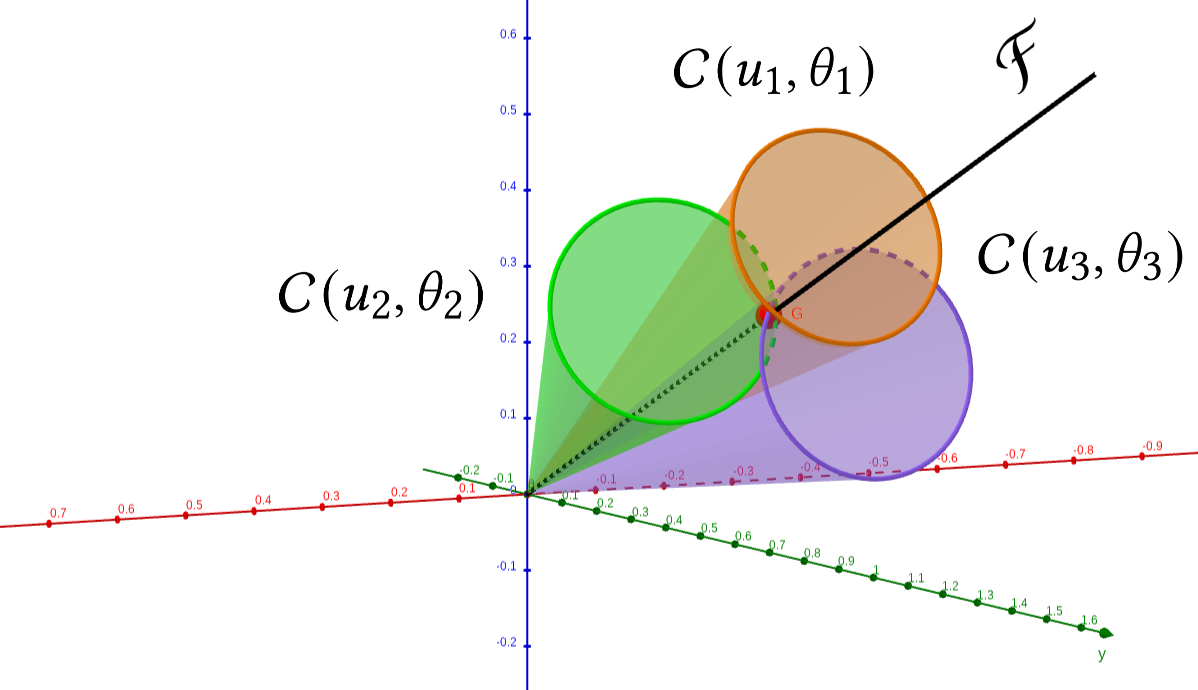
Threat model
- Attacker: honest‑but‑curious dominant client (or server)
- Knows:
- Unit buffer vectors \(u_1,\dots,u_k \in \mathbb{R}^d\)
- Cosines \(c_i = u_i^\top y\) with unknown unit \(y\)
- Goal: recover the direction of \(y\), then use metadata to reconstruct the point
Stack constraints as \(U y = c\), where \(U \in \mathbb{R}^{k \times d}\) has rows \(u_i^\top\) and \(c \in \mathbb{R}^k\). - If \(k=d\) and \(U\) is nonsingular: \(y = U^{-1} c\), then normalize. - Else: use least squares; normalize to get a direction. - Complexity: \(O(d^3)\) once for inversion; then \(O(d^2)\) per point.
Worked example (BMI toy)
Fields: Gender \(\in \{-1,+1\}\), Height (cm), Weight (kg).
Given \[ U=\begin{bmatrix} -0.0046 & 0.7558 & 0.6550\\ \phantom{-}0.0040 & 0.7976 & 0.6032\\ -0.0046 & 0.7276 & 0.6858 \end{bmatrix}, \qquad c=\begin{bmatrix}0.9513\\0.9697\\0.9376\end{bmatrix}. \]
Phase 1 (direction): solve \(Uy=c\) and normalize: \[ y \approx (-0.00610,\ 0.9207,\ 0.3902), \qquad \mathcal{F}(t)=t\,(0.00610,\ 0.9207,\ 0.3902). \]
Phase 2 (metadata): Let gender \(g\in\{-1,+1\}\). Scale by \(\alpha=g/y_1\), set \(p=\alpha y\), then replace \(p_1\) with \(g\). Candidates: \([-1,151,64]\) and \([1,-151,-64]\). Plausible ranges (positive height/weight) select \([-1,151,64]\).
Minimal NumPy demo
#| echo: true import numpy as np
def reconstruct_direction(U, c): y_hat, *_ = np.linalg.lstsq(U, c, rcond=None) return y_hat / np.linalg.norm(y_hat)
def reconstruct_with_metadata(y_dir, gender): alpha = gender / y_dir[0] p = alpha * y_dir p[0] = gender return p
U = np.array([ [-0.0046, 0.7558, 0.6550], [ 0.0040, 0.7976, 0.6032], [-0.0046, 0.7276, 0.6858],], dtype=float)
c = np.array([0.9513, 0.9697, 0.9376], dtype=float)
y_dir = reconstruct_direction(U, c) p_gneg = reconstruct_with_metadata(y_dir, gender=-1) p_gpos = reconstruct_with_metadata(y_dir, gender=+1)
print(“Direction:”, np.round(y_dir, 6)) print(“Candidate (g=-1):”, np.round(p_gneg, 1)) print(“Candidate (g=+1):”, np.round(p_gpos, 1))
Where it appears in FLICKER
- During resampling, the dominant client learns cosines between other clients’ points and its buffer vectors. In low \(d\), enough independent constraints across rounds identify directions.
- Server variant: if buffer vectors and cosines are encrypted under the server’s public key, a curious server can decrypt and reconstruct similarly.
Mitigations
- Avoid low‑dimensional feature sharing; in high \(d\), getting \(k=d\) independent directions is much harder.
- Keying changes to stop server‑side recovery: – Client‑side HE key generation (each client keeps its secret key) – Server stores only evaluation keys; never decrypts – Round‑based key provisioning for the dominant client only
- Reduce cosine leakage: aggregate/coarsen values, clip, and/or fewer rounds.
- Audit independence of buffer directions to estimate reconstruction risk.